++ 50 ++ y x graph shade 157131-Y x graph shade

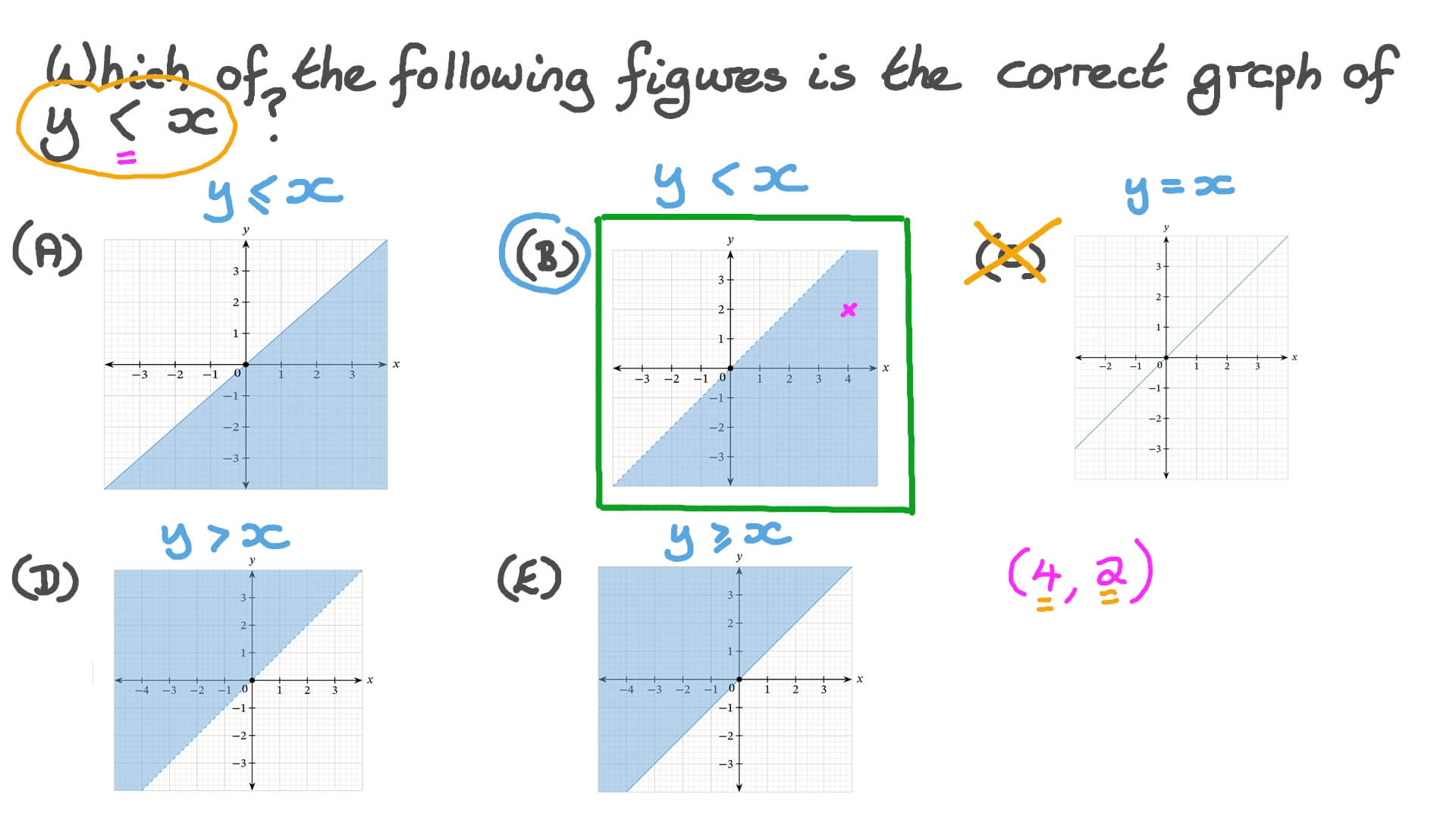
The solution is y ≥ x and y ≤ x 4 We shade above the line y = x and below the line y = x 4 13) What is the set of all points (x, y) that is a solution to the system of inequalities?Graph and shade the region enclosed by the curves x = (y 2) ^2 and y = x What is the volume of the solid obtained by rotating the shaded region about the line y =1 explaining the geometry Draw the figure Determine the points where these two graphs intersect Let these points be Q and R, with the X coordinate of Q being lesser than the X coordinate of R Determine two points by substituting values for x and solving for y Then plot the points and draw a dashed straight line through the points to indicate that they are not part of the inequality Shade in the area above the line x = 0, y = − 3

Draw The Graphs Of Y X 1 And X Y 5 On The Same Cartesian Plane Shade The Triangle Formed By These Graphs And Y Axis And Also Find Its Area

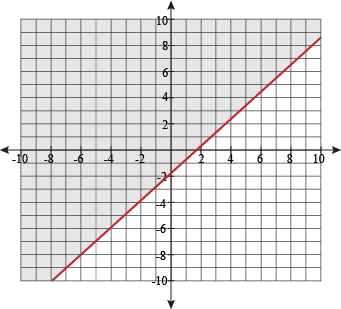
Y x graph shade

Y x graph shade-The solution of the system is the region where all the shaded parts overlap Here is a different method For each inequality, shade the region that does not satisfy the inequality1 Graphing Linear Inequalities Notation x y means x is less than or equal to y x y means x is greater than or equal to y x < y means x is less than y x > y means x is greater than y The last two inequalities are called strict inequalities Our focus will be on the nonstrict inequalities Algebra of Inequalities Suppose x3 < 8

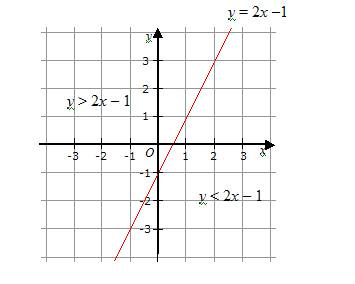
Graphing Inequalities Solutions Examples Videos

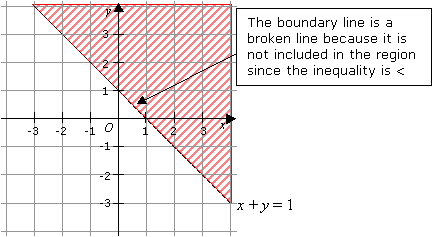
Example By shading the unwanted region, show the region represented by the inequality x y < 1 Solution Rewrite the equation x y = 1in the form y = mx c x y = 1 can be written as y = –x 1 The gradient is then –1 and the yintercept is 1 We need to draw a dotted line because the inequality is < After drawing the dotted line, we need to shade the unwanted region The graph of the equation y = x 2 6x 12 is the boundary of the region Since the inequality symbol isGraphing Systems of Linear Inequalities To graph a linear inequality in two variables (say, x and y ), first get y alone on one side Then consider the related equation obtained by changing the inequality sign to an equality sign The graph of this equation is a line If the inequality is strict ( < or > ), graph a dashed line

 She uses a graphing program to graph the equations y = 23 – 5x and y = 10 – 2x Use the graph to find the solution of 23 – 5x = 10 – 2x Line graph with 2 lines X axis ranges from negative 10 to 10; For exercises 14 19, graph the equations and shade the area of the region between the curves If necessary, break the region into subregions to determine its entire area 14) y = sin(πx), y = 2x, and x > 0 15) y = 12 − x, y = √x, and y = 1 Answer 34 3 units 2If the point is a solution, shade the portion of the graph containing the test point If not, shade the other side of the line Example 1 Graph the inequality y < x Solution Replace the inequality symbol with an equal sign and graph the related equation y = x

Sketch and shade the region bounded by the graphs of the functions Graphing Functions The graph of a function {eq}y = f(x) {/eq} is the set of all points {eq}(x,yThe following equations y = x2 9 y = x 5 X = 0 x = 2 Sketch and shade the region bounded by the graphs of the functions (Use solid lines for the 40 Graph Lay After you 구 can use G 6 properties Fill 4 3 4 2 No Solution 7 40 Help WebAssignThe graph of the line x y = 5 divides the plane into three parts the line itself and the two sides of the lines (called halfplanes) x y 5 is a halfplane x y 5 is a line and a halfplane If one point of a halfplane is in the solution set of a linear inequality, then all points in that halfplane are in the solution set This gives

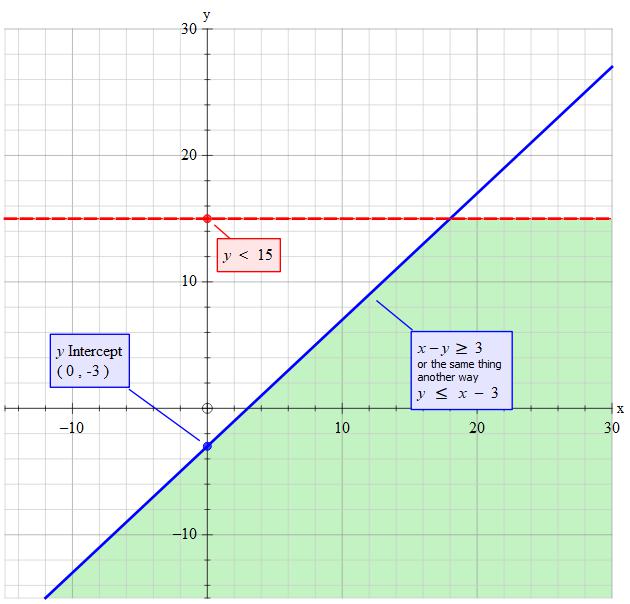
How Do You Graph The System Of Linear Inequalities X Y 3 And Y 15 Socratic

Draw The Graphs Of Y X 1 And X Y 5 On The Same Cartesian Plane Shade The Triangle Formed By These Graphs And Y Axis And Also Find Its Area

This method of drawing the graph of a linear equation is called the intercept method of graphing Note that when we use this method of graphing a linear equation, there is no advantage in first expressing y explicitly in terms of x Example 1 Graph 2x y = 6 by the intercept method SolutionClick here👆to get an answer to your question ️ Draw the graph of x 2y 7 = 0 & 2x y 4 = 0 Shade the area founded try these lines Y axisAvail 25% off on study pack Avail Offer

1

Linear Inequalities And Half Planes

Graph the solution to the following system of inequalities y > 3 x 2 Y < 4x 7 Everytime I create the graph my shading is wrong I do not understand how to shade it correctly Graph the equation y = x − 6 then shade the side of the graph for which y ≤ x −6 is trueGraph one inequality First graph the boundary line, then test points Remember, because the inequality 3 x 2 y < 12 3 x 2 y < 12 does not include the equal sign, draw a dashed border line Testing a point like ( 0, 0) ( 0, 0) will show that the area below the line is

Graphing Linear Inequalities

Graphing Linear Inequalities Section 6 8 Everyone Get A Communicator One Side Blank Other Side Graph Ppt Download

Since y is less than the expression, you will shade below the line If you are unsure of which side to shade, pick any point on the graph (that's not on the line) You are choosing a test point to determine which side contains the solutions I will choose (0,0) because this is the easiest point to substitute into the inequality to check forGraphing Quadratic Inequalities A quadratic inequality of the form y > a x 2 b x c (or substitute < , ≥ or ≤ for > ) represents a region of the plane bounded by a parabola To graph a quadratic inequality, start by graphing the parabolaShading Graphs To shade a graph, you must first graph the function To do this you must first have the function in the form of y = Remember when working with inequalities you flip the inequality if you ever multiply or divide by a negative number Enter the function into the graphing

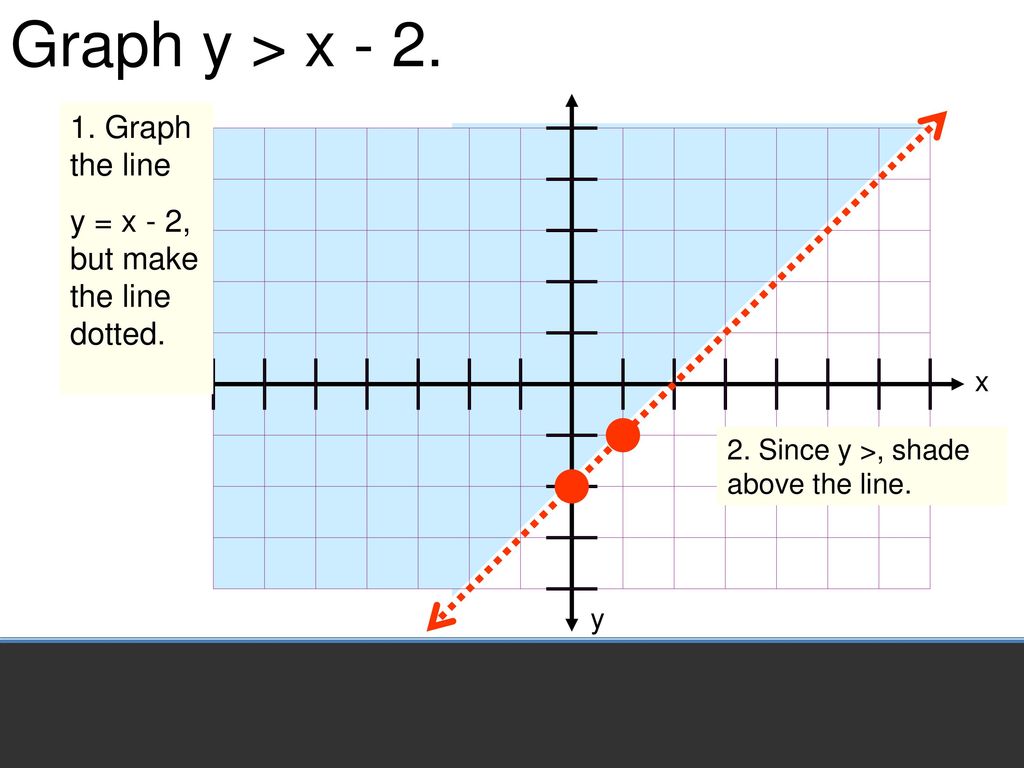
Graphing Linear Inequalities Ppt Download

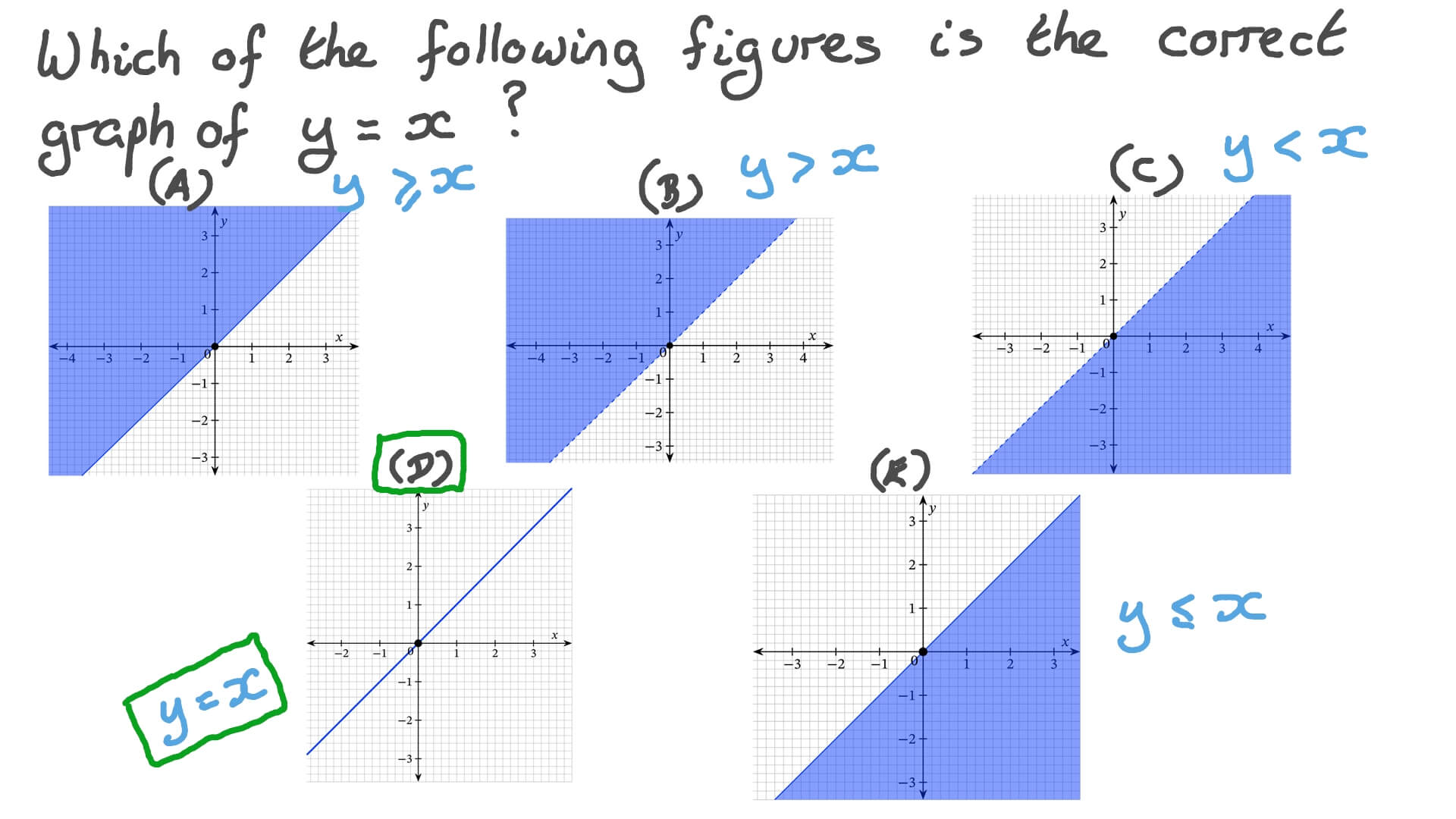
Question Video Graphs Of Linear Inequalities Nagwa

Axis choice options associate the plot with a particular y or x axis on the graph;How to graph your problem Graph your problem using the following steps Type in your equation like y=2x1 (If you have a second equation use a semicolon like y=2x1 ;Shade the Draw the graphs of the equations `xy=1\ a n d\ 2xy=8` Shade the area bounded by these two lines and yaxis Also, determine this area

Graphing Inequalities X Y Plane Review Article Khan Academy

Graphing Linear Inequalities

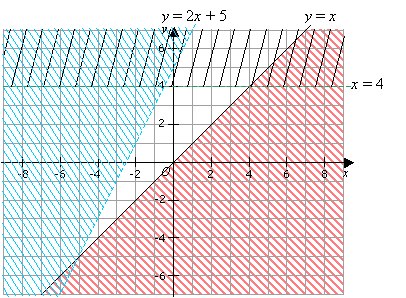
Draw the Graph for 3x y = 3 and x 2y = 4 and shade the region bounded with the x axis BOLPANGMAIa Channelko namdapatna dakchakpana skode kamao ongipStep 3 Now graph the y = x 1 Use the method that you prefer when graphing a line In addition, since the original inequality is strictly greater than symbol, \Large{\color{red}>}, we will graph the boundary line as a dotted line Step 4 The original inequality is y > x 1 The greater than symbol implies that we are going to shade the topGraph each inequality y < x í 3 62/87,21 y < x í 3 Because the inequality involves

Learning Task 4 1 Graph The T See How To Solve It At Qanda

23 Let R Be The Shaded Region Bounded By The Graph Chegg Com

 Draw the graphs of the lines xy=1 and 2xy=8 Shade the area formed by two lines and the yaxis Also,find the areaBoth lines cross x, y axes;Graph of an Inequality When we were dealing with one variable, the graph of an inequality was some interval on the real number line Now we are dealing with two variables, and the graph of an inequality is the set of all ordered pairs (x, y) that satisfy the inequality Typically, this will be represented by a halfplane

In The Graph Y Is Less Than Or Equal To X Which Quadrant Is Completely Shaded Brainly Com

Graphing Linear Inequalities

 Question (a) Sketch the graph of the function y = x² and shade the region between thegraph of the function and the line y = 4x – 3 (b) Calculate the area shaded in Qn5 (a)Shade the triangle formed by the graphs of 2x – y = 4, x y = 2 and the yaxis Write the coordinates of vertices of the triangle Now draw a graph of y = 2x/3 – 2 and shade below the line Example 4 x y < 1 Solution Rewrite the equation x y = 1 to make y the subject of the formula Because the inequality sign is

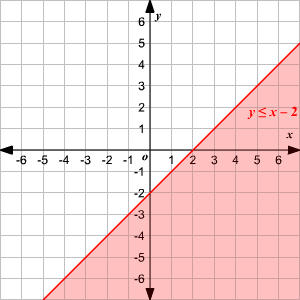
Graphing Systems Of Linear Inequalities

Ixl Solve Systems Of Linear Inequalities By Graphing Algebra 1 Practice

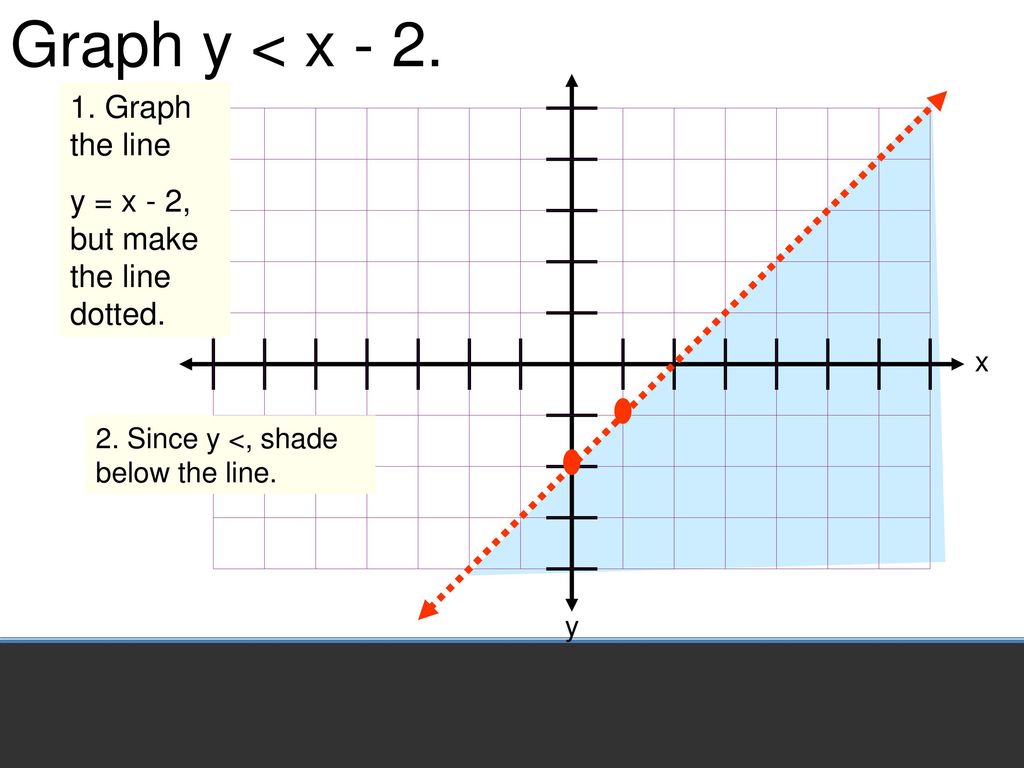
Find The Area Between Y=x And Y=x Graph Region And Shade The Area 2 (50 Points) Set Up An Integral For Each Of The Following Evaluate That Integral To Find The Volume Of The Solid Obtained By Rotating The Region Bounded By Y=x And Y=8 In The First QuadrantSolve each system of inequalities by graphing x y x í 3 62/87,21 *UDSK HDFK LQHTXDOLW\ The graph of x LV VROLG DQG LV LQFOXGHG LQ WKH JUDSK RI WKH VROXWLRQ The graph of y x í 3 is also solid and is included in the graph of the solution 7KH VROXWLRQ RI WKH V\VWHP LV WKH VHW RI RUGHUHG SDLUV LQ WKH LQWHUVHFWLRQ RI WKH JUDSKV RI x DQG y x íGraph of inequality y < x – 3 To check to see whether you've shaded the correct half‐plane, plug in a pair of coordinates—the pair of (0, 0) is often a good choice If the coordinates you selected make the inequality a true statement when plugged in, then you should shade the half‐plane containing those coordinates

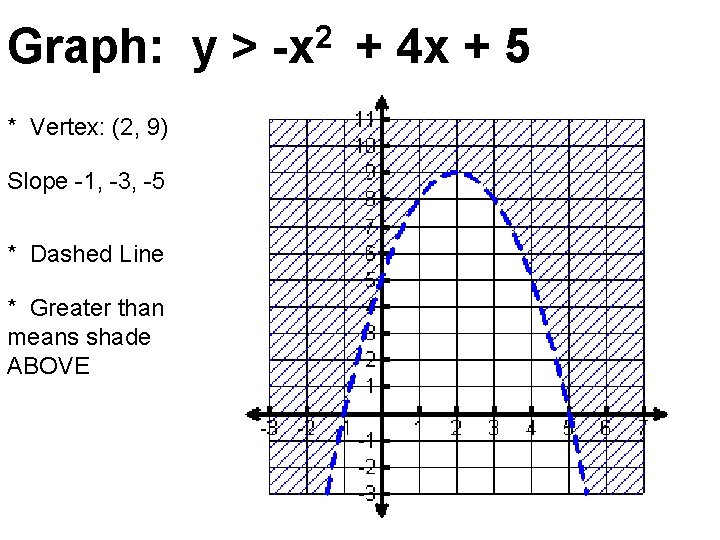
Graphing Quadratic Inequalities Steps For Graphing Quickly Shading

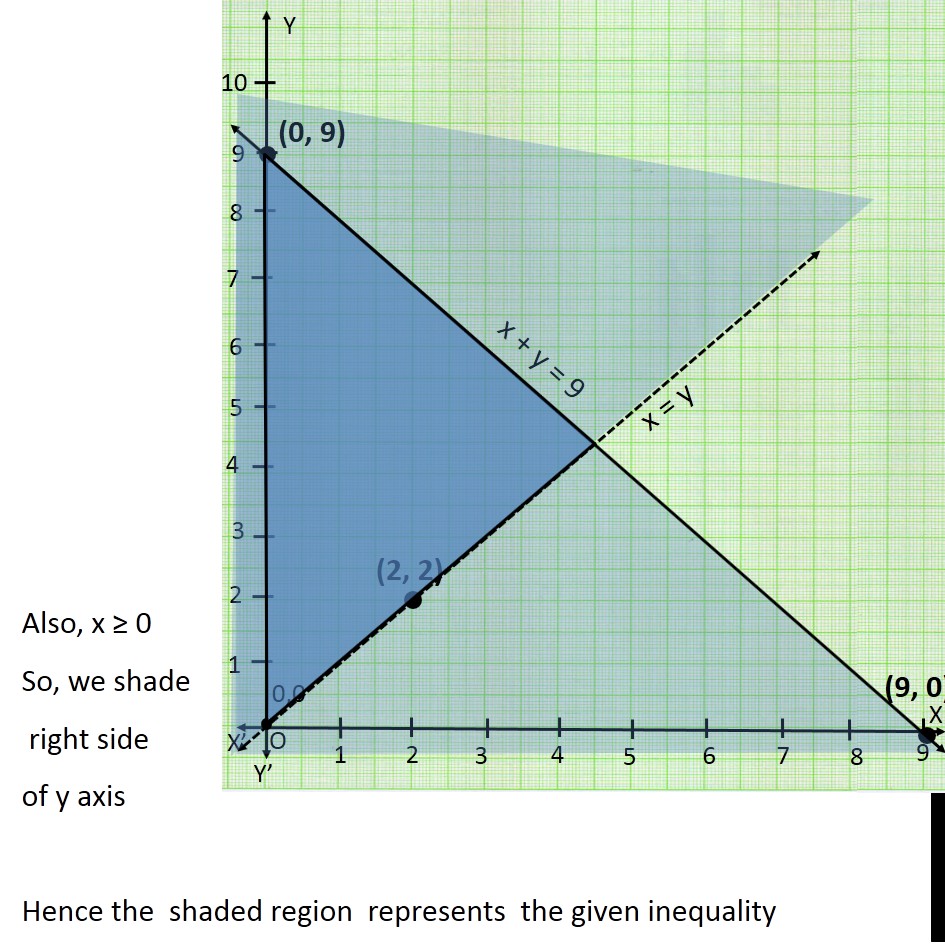
Ex 6 3 8 Solve X Y 9 Y X X 0 Graphically Ex 6 3

Y=x3) Press Calculate it to graph!Intersect at (negative 41, 1)Let's graph another inequality latexy>−x/latex You can check a couple of points to determine which side of the boundary line to shade Checking points M and N yield true statements

Graphing Systems Of Inequalities

Ex 6 3 8 Solve X Y 9 Y X X 0 Graphically Ex 6 3

2x 5y > 10 4x 6y ≤ 12 x > 0 A) The point (15 4,1 2)Shading Unwanted Regions To graph the solution of a system of inequalities, we have shaded the solution of each inequality in a different color; draw the graphs of the following equations x y 5 x y 5 i find the solution of the equations from the graph ii shade the triangular region formed by th Mathematics TopperLearningcom rmtc0aktt Starting early can help you score better!

Gcse Maths Inequalities Write Inequalities Which Define The Shaded Region Inequalities On Graphs Youtube

Graphing Inequalities Solutions Examples Videos

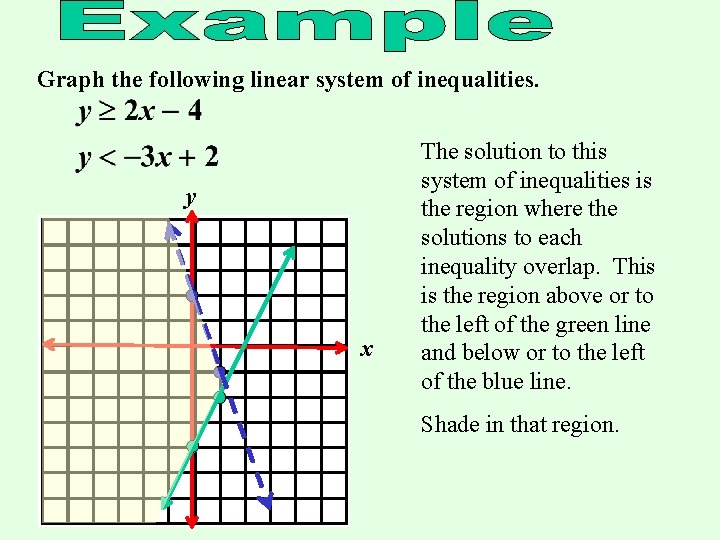
1 Graph and shade the region enclosed by the curves y=(x3)* and y=x Find the volume of the solid obtained by rotating the shaded region about the line x=I explaining the geometry 2 Determine whether the improper integral Hence evaluate the integral Tx(x 9) converge or diverge 3 Sketch the graph of the limacon r = 32cos and the circle r= 2 Shade (b) Step 1 The system of inequalities are and Graph the all of four constraints Draw the coordinate plane Consider the inequality Graph the line Since the inequality symbol is , the boundary is included the solution set Graph the boundary of the inequality with solid line To determine which half plane is to be shaded, consider a test point in either of the half planeAnswer to Shade the intersection of graphs 2x y \\le 4 and x 2y greater than 6 By signing up, you'll get thousands of stepbystep solutions

Graphing Linear Inequalities Examples Chilimath

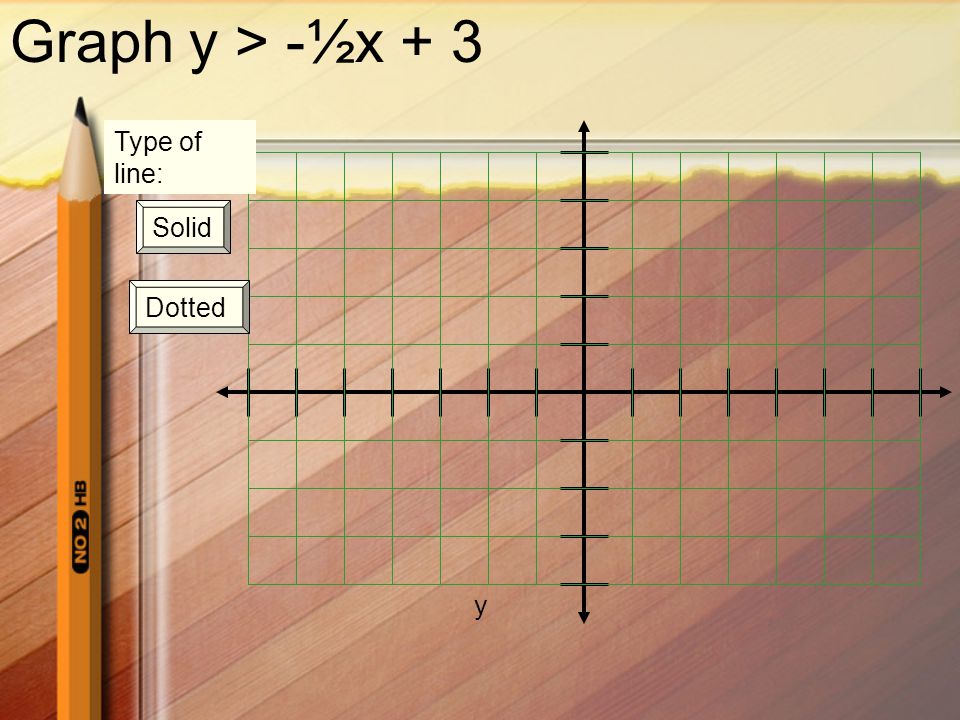
Graphing Linear Inequalities Section 6 8 Everyone Get A Communicator One Side Blank Other Side Graph Ppt Download

 Shade in one side of the boundary line If the test point is a solution, shade in the side that includes the point Identify the x– and yIntercepts on a Graph In the following exercises, find the x– and yintercepts Find the x– and yIntercepts from an Equation of a LineSee G3 axis choice options twoway options are a set of common options supported by all twoway graphs These options allow you to title graphs, name graphs, control axes and legends, add lines and text, set aspect ratios,Graph yx=4 y − x = 4 y x = 4 Add x x to both sides of the equation y = 4 x y = 4 x Rewrite in slopeintercept form Tap for more steps The slopeintercept form is y = m x b y = m x b, where m m is the slope and b b is the yintercept y = m x b y = m x b Reorder 4 4 and x x

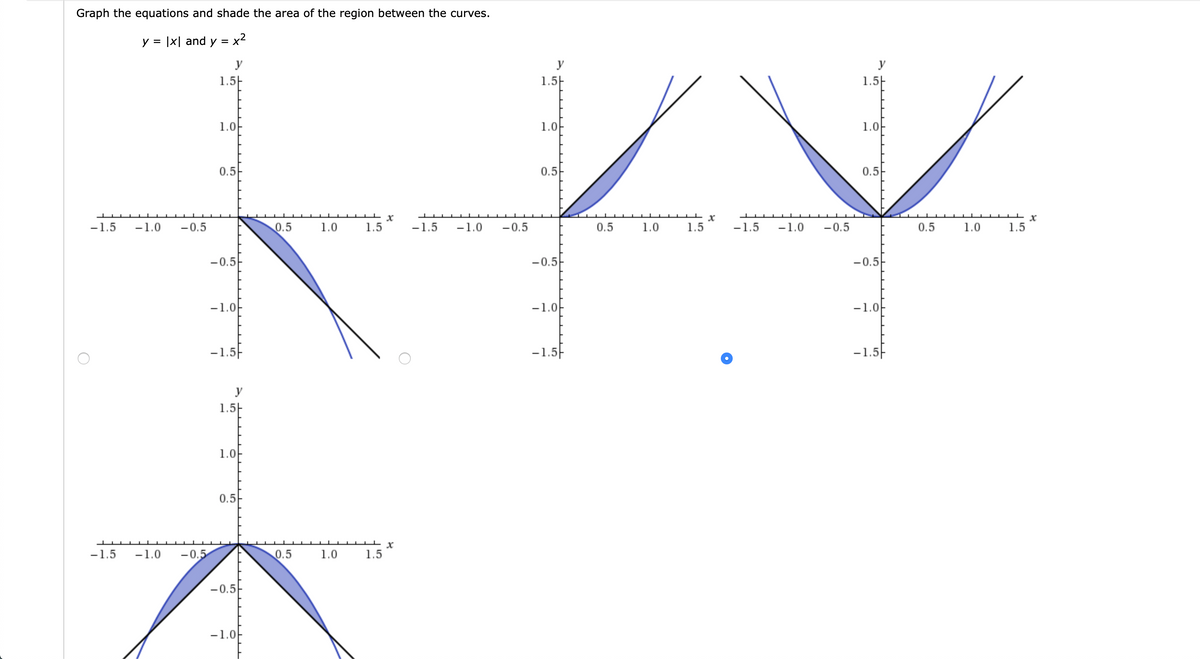
Answered Graph The Equations And Shade The Area Bartleby

Graphing Linear Inequalities Ppt Download

Transcribed Image Text (a) Graph and shade the region enclosed by the curves y = 2x and y = x (b) Determine the volume of the solid obtained by rotating the shaded region about the line y = 1 along with the explanations of the geometryGraphing the line y = x 3 on a Cartesian Graphgraph the function y=x3 Graphing the line y = x 3 on a Cartesian Graphgraph the function y=x3Y axis range from 6 to negative 6;

Inequalities Graphing Inequalities Sparknotes

Graph For Y X 3 Novocom Top

Do not pass through origin; The first line, y=x1, is greater than, so we will shade above the line The second inequality is less than, so we will shade below the line Since this system is connected by an "and," we will only shade the overlap of these two inequalities, shown in purple below Graph the solid boundary line, y ≤ x 1 and shade below it Graph the solid boundary line y ≥ –2x 4, and shade below it The overlapping region is the solution region The solution is a triangle 24 Holt Algebra 2 33 Solving Systems of Linear Inequalities Lesson Quiz Part I 1 Graph the system of inequalities and classify the figure

Graphing Linear Inequalities Teacher Guide

Find The Area Of The Shaded Region Y X 2 3 Study Com

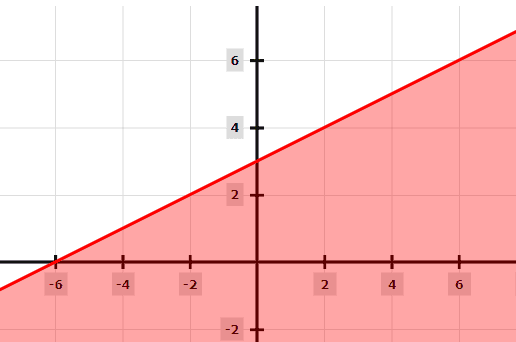
Graphing Linear Inequalities Explanation Examples

Inequalities Graphing Inequalities Sparknotes

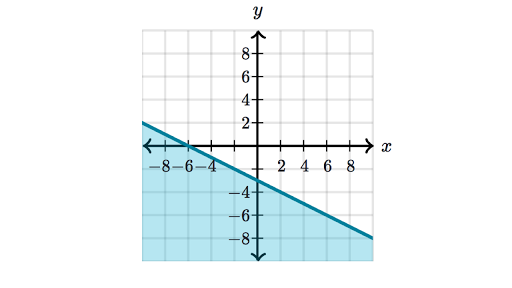
Graphing Inequalities X Y Plane Review Article Khan Academy

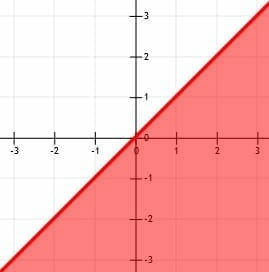
Graphing Linear Inequalities Explanation Examples

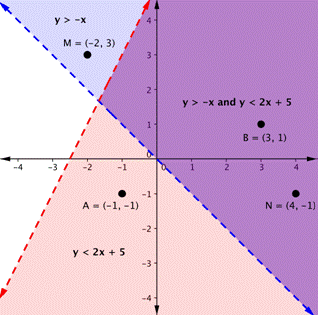
Graphs And Solutions To Systems Of Linear Equations Beginning Algebra

Integration Area And Curves

Question Video Graphs Of Linear Inequalities Nagwa

Look At The Two Graphs Determine The Following

Graphing Systems Of Linear Inequalities

Graph Each Inequality 1 Y X 3 Solution Waynesville R

Graphing Inequalities Solutions Examples Videos

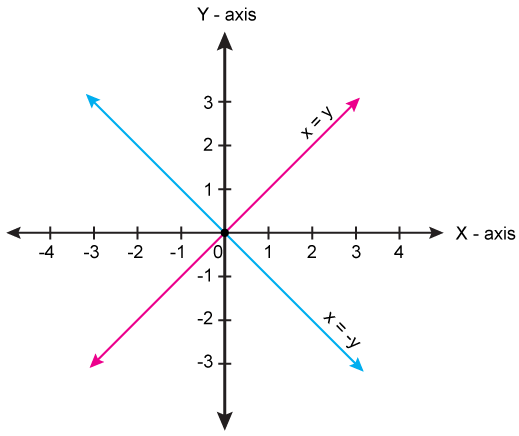
Draw The Group Line Y X And Y X On Same Graph To Shade Format At Triangle And Y Axis Also Find The Area Mathematics Topperlearning Com Srohfz11

Graphing Inequalities X Y Plane Review Article Khan Academy

Solution A Convert The Inequality X Y Gt 7 To Slope Intercept Form B Graph The Inequality In The Space Provided At The Right You May Use Any Method To Fine The

How Do You Graph The Inequality Y 3 Socratic

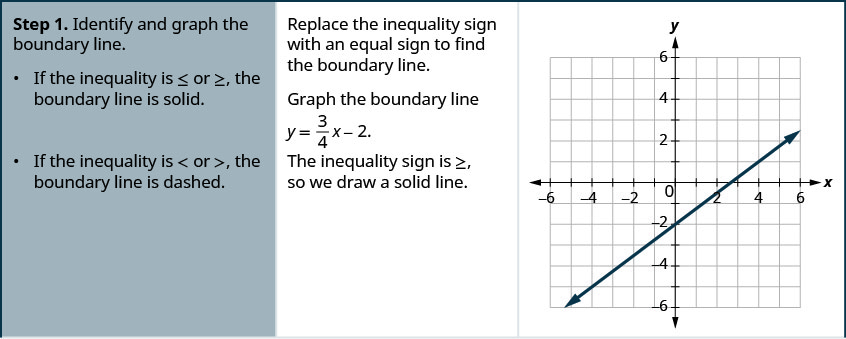
4 1 Graphing Linear Inequalities In Two Variables Mathematics Libretexts

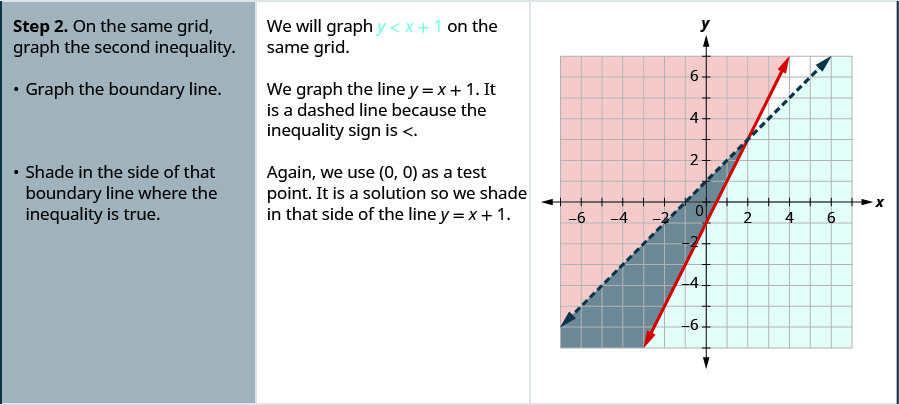
4 2 Graphing Systems Of Linear Inequalities Mathematics Libretexts

How Do You Graph Y X 2 Color White D Y 3x 2 Socratic

1

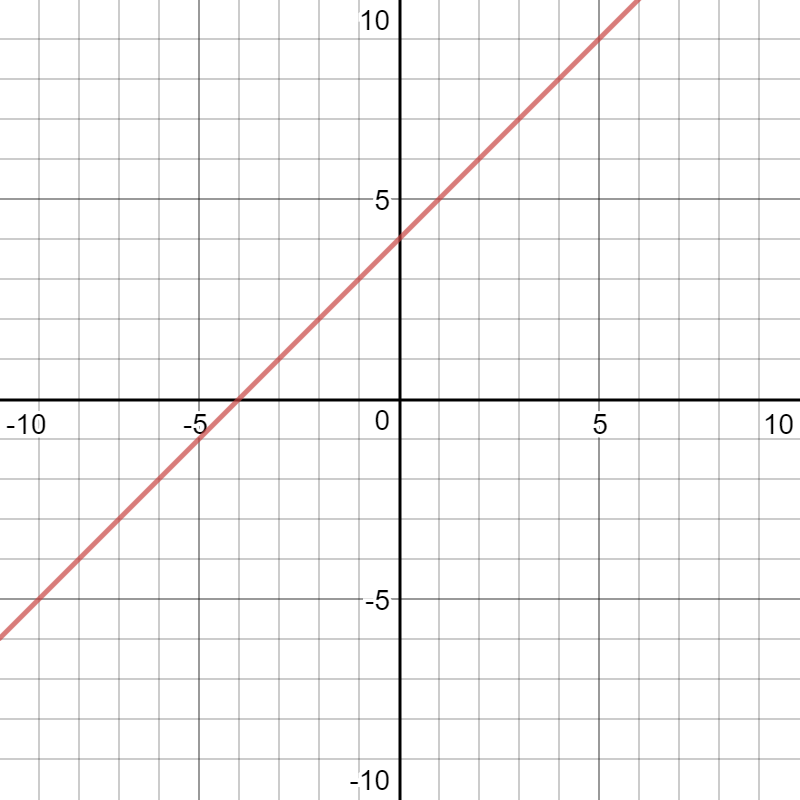
How Do You Graph The Inequality Y X 4 And Y 6x 3 Socratic

System Of Inequalities Graphing Concept Video Lesson Transcript Study Com

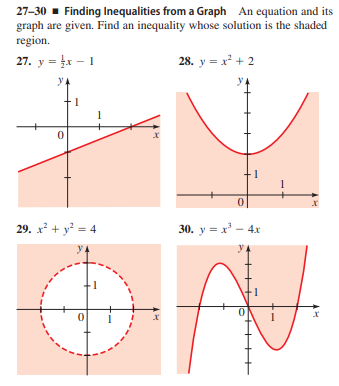
Answered 27 30 Finding Inequalities From A Bartleby

2 Shade The Region Where Descubre Como Resolverlo En Qanda

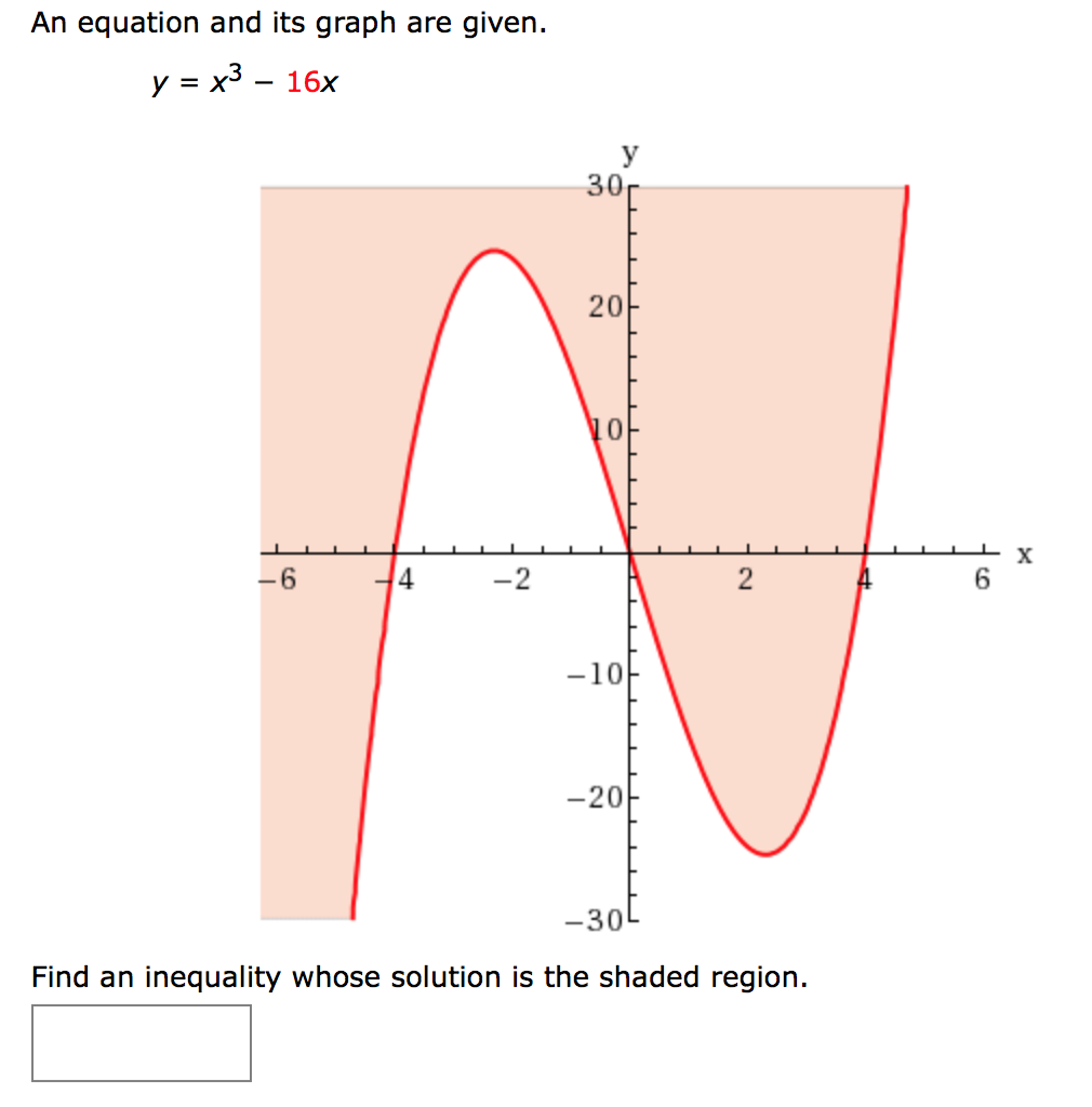
An Equation And Its Graph Are Given Y X 3 16x Chegg Com

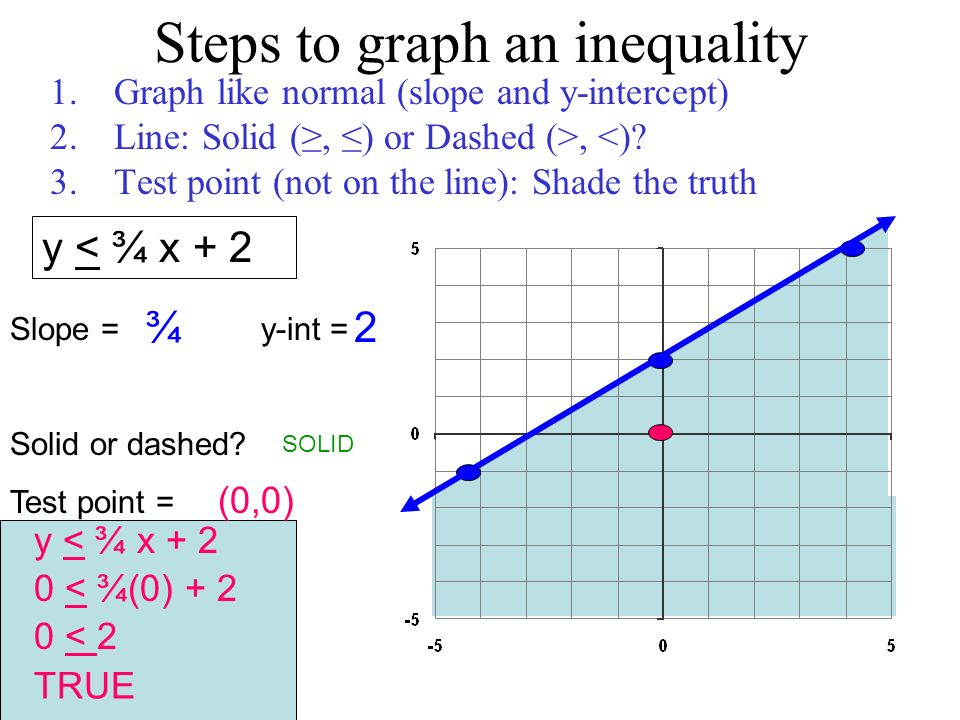
Section 6 5 Linear Inequalities Is The Ordered Pair A Solution For Y X 3 A 1 2 How Do We Know If 1 2 Is A Solution Y X 3 Ppt Download

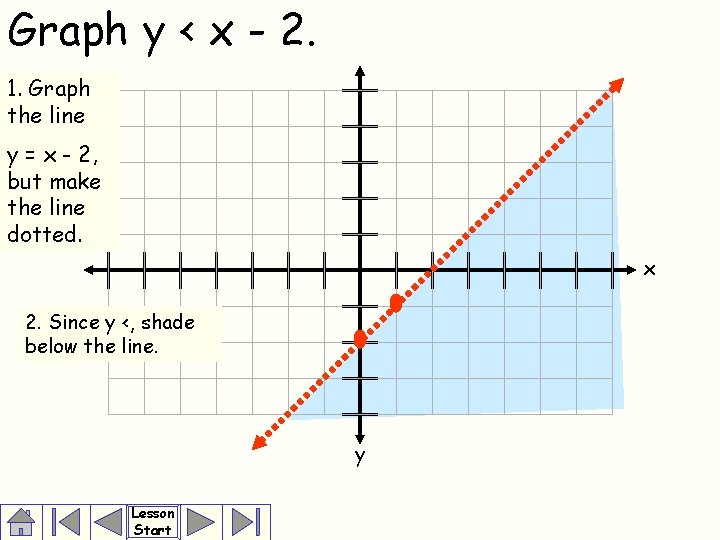
Linear Inequalities Linear Equations Drive On The Education

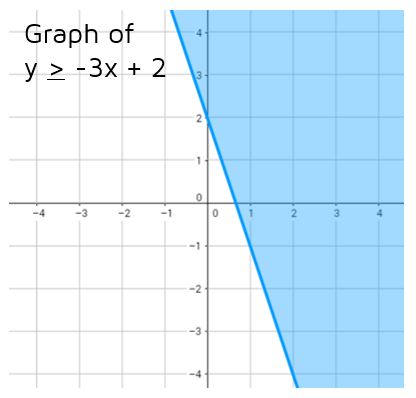
Graphing Linear Inequalities Kate S Math Lessons

Algebra 6 5 Graphing Linear Inequalities Linear Inequality

Graphing Linear Inequalities

Graph The Linear Inequality Y X Study Com

E9zc0qhlevm2sm

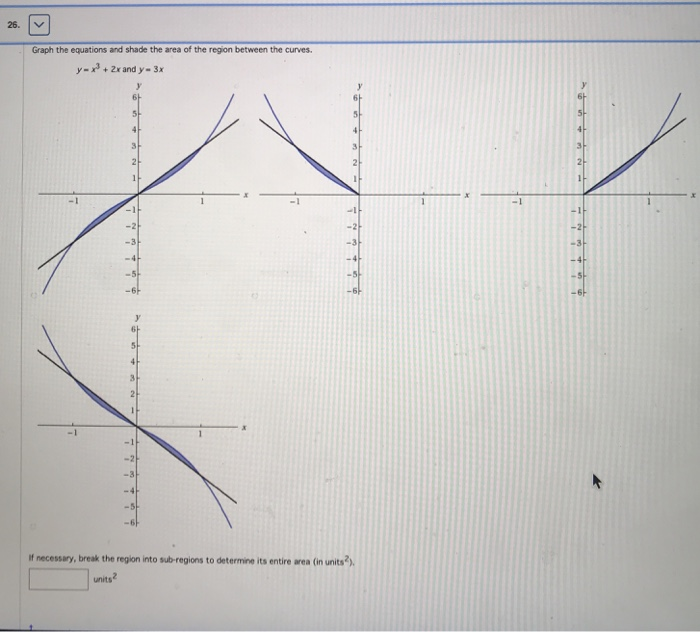
Solved 26 Graph The Equations And Shade The Area Of The Chegg Com

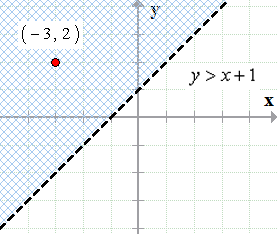
Graphing Linear Inequalities Chilimath

Graphing Linear Inequalities

01 Graphing Inequalities In Two Variables Part 1 Solve Graph Shade Inequalities Youtube

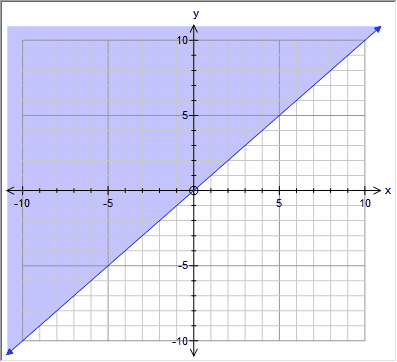
Graph Other Preferences

Graphing Systems Of Inequalities

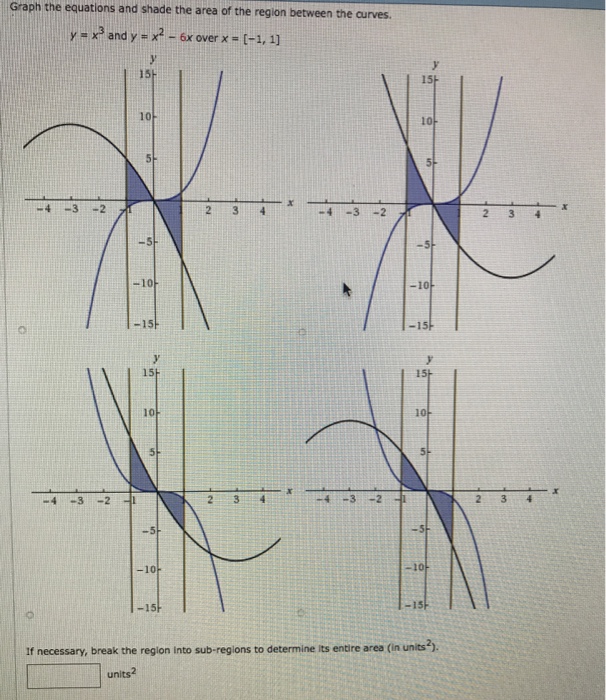
Graph The Equations And Shade The Area Of The Region Chegg Com

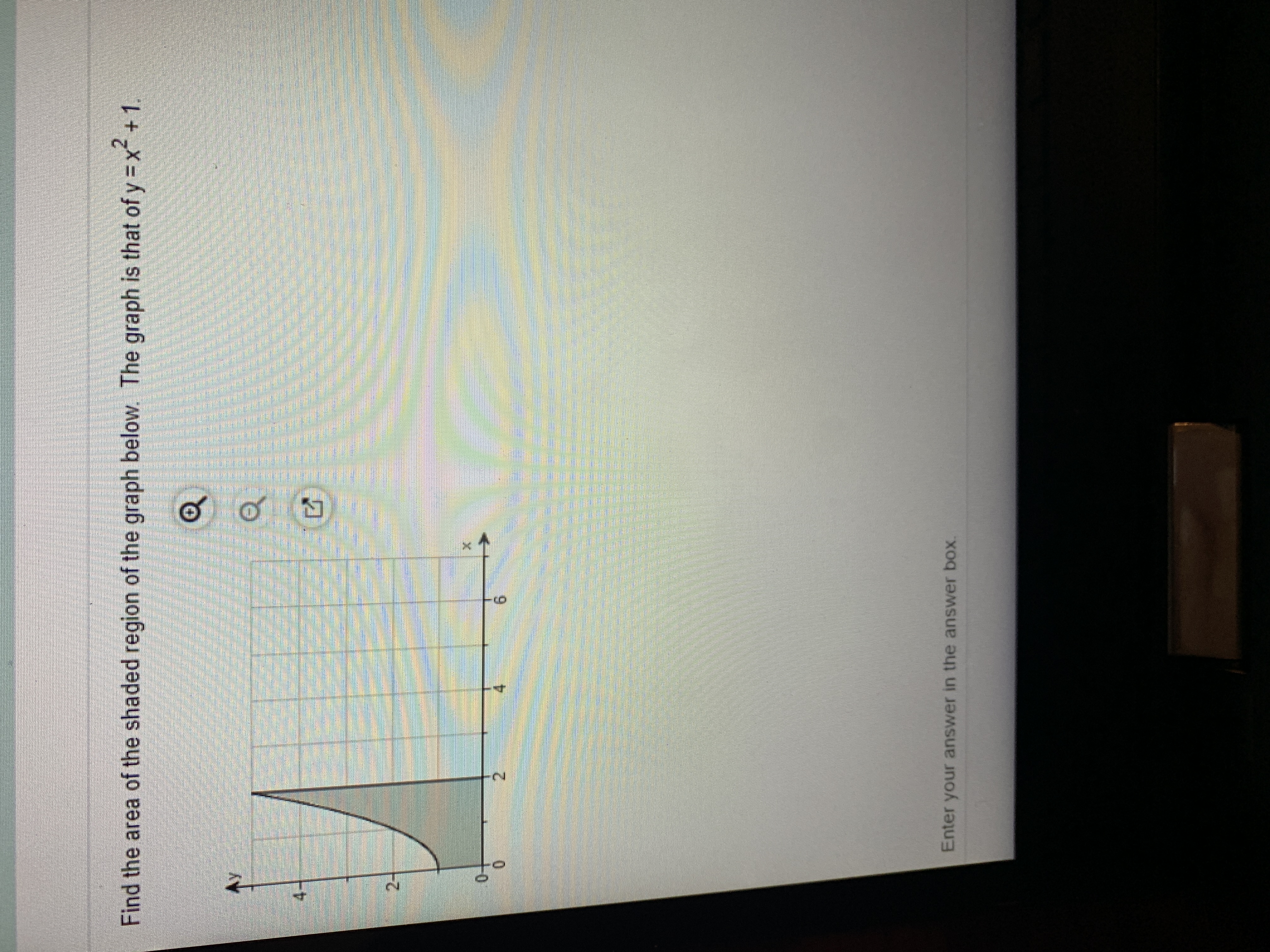
Answered Find The Area Of The Shaded Region Of Bartleby

How To Graph A System Of Inequalities Algebra House

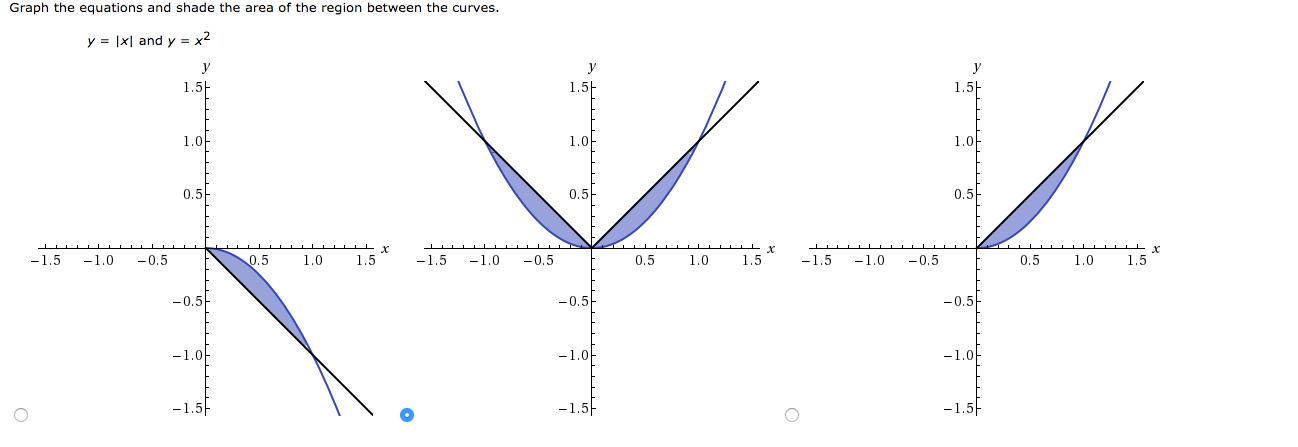
Graph The Equations And Shade The Area Of The Region Chegg Com

Y X 2 6x 12 Graphed And Shade The Side That Needs To Be Shaded Mathskey Com

How Do You Graph The System Of Linear Inequalities Y 1 X 1 And Y X 1 Socratic

2 Shade The Region Where Descubre Como Resolverlo En Qanda

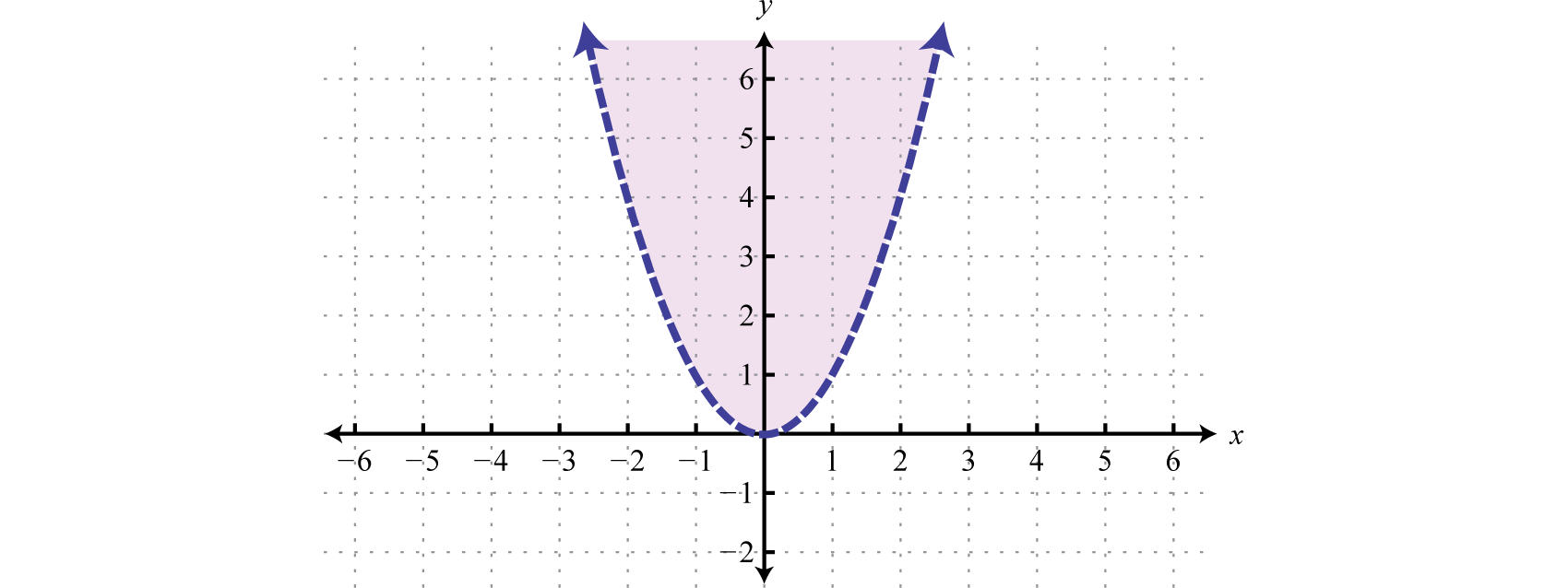
Solving Inequalities With Two Variables

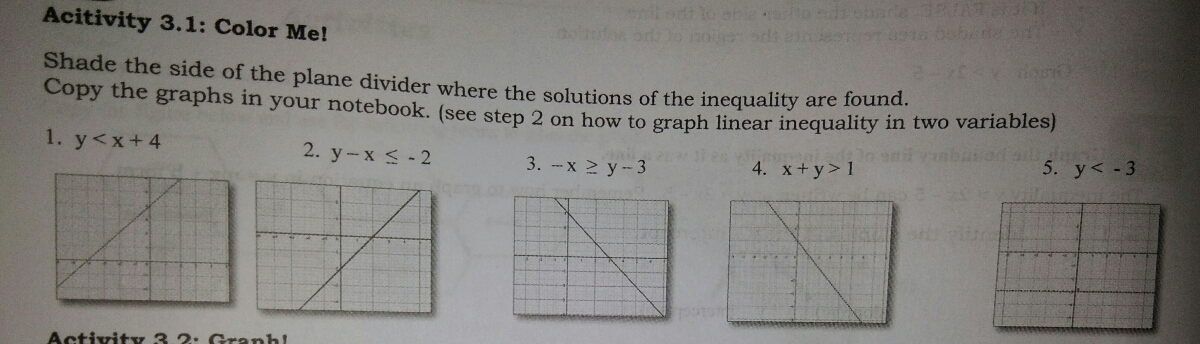
Answered Shade The Side Of The Plane Divider Bartleby

Module 5 Inequalities

Graphing Linear Inequalities

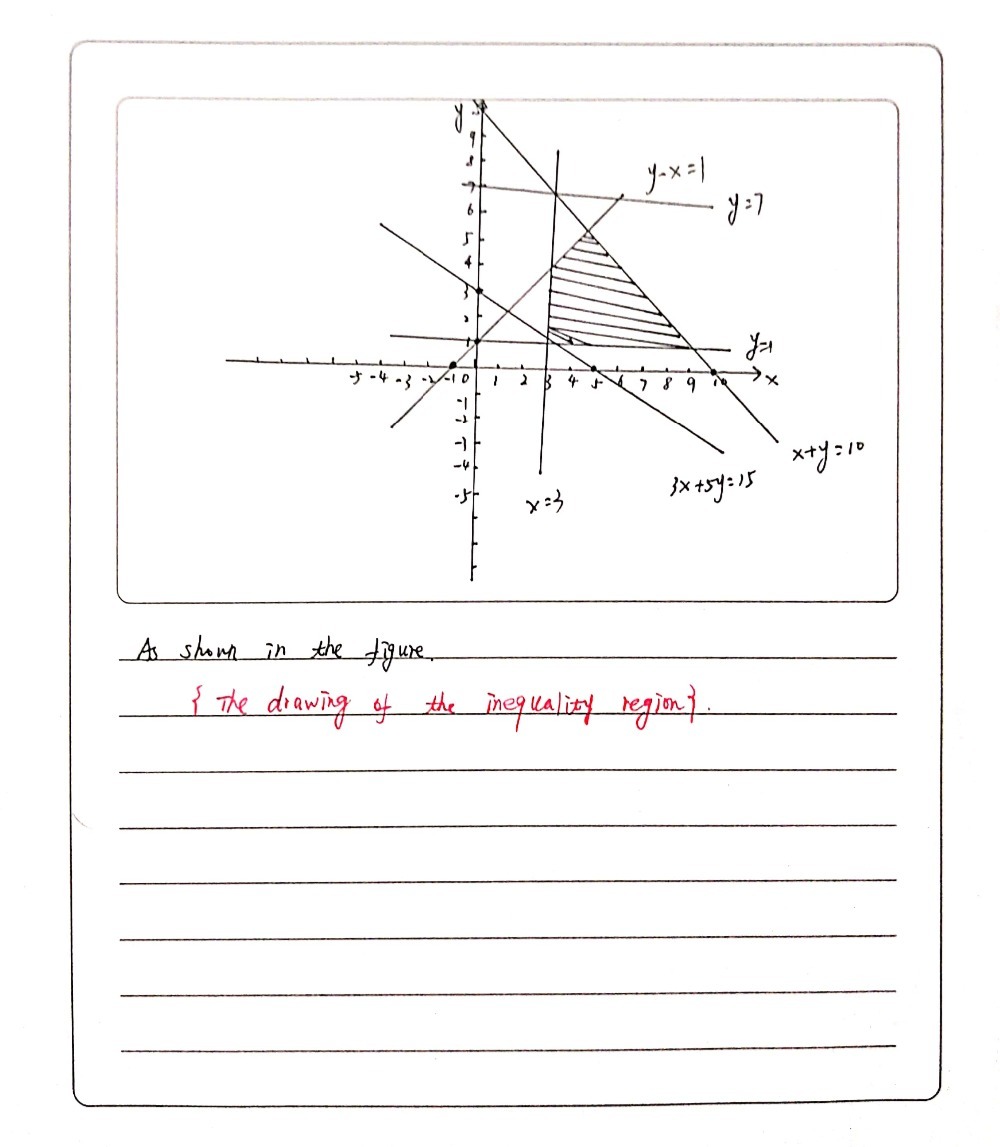
Question 2 Shade The Region That Satisfies The Fol Gauthmath

How Do You Graph The System Of Inequalities X 0 Y 0 X Y 2 0 Socratic

Graph Inequality On Coordinate Plane Youtube

Draw The Graph Of Y X 1 Amp X Y 5 On The Same Cartesian Plane Shade The Triangle Formed By These Brainly In

Graphing Systems Of Inequalities

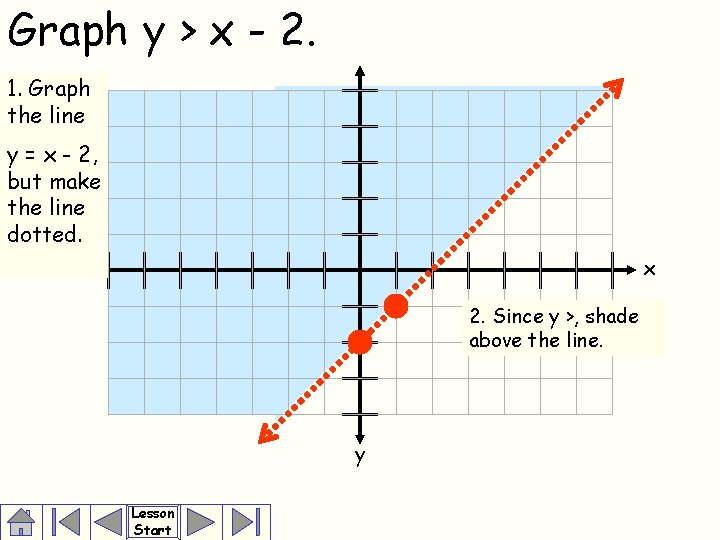
Linear Inequalities Linear Equations Drive On The Education

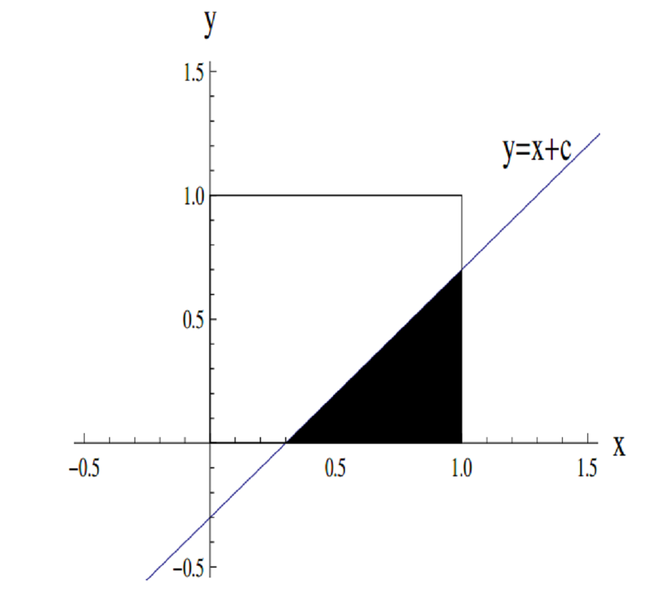
Solution Which Of These Graphs Shows The Area A C As C Varies Geometry Of Equations Underground Mathematics

Graphing Linear Inequalities

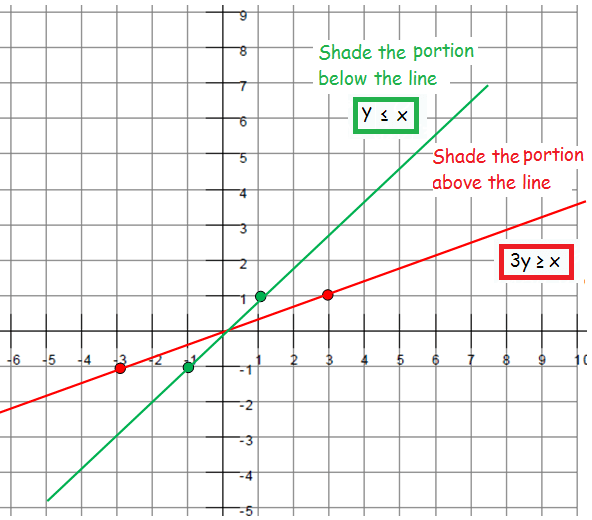
Graphing Linear Inequalities In Two Variables And Find Common Region

Graphing Systems Of Linear Inequalities Ck 12 Foundation

Systems Of Linear Inequalities At A Glance

Graphing Linear Inequalities

Draw The Graph Of Y X 1 And X Y 5 On The Same Cartesian Plane Shade The The Triangle Formed By These Brainly In

Q Tbn And9gctpbm6wmtmjhsuco3taeyxvnarnhw Rd F2pd3 P1czdbeupzzy Usqp Cau

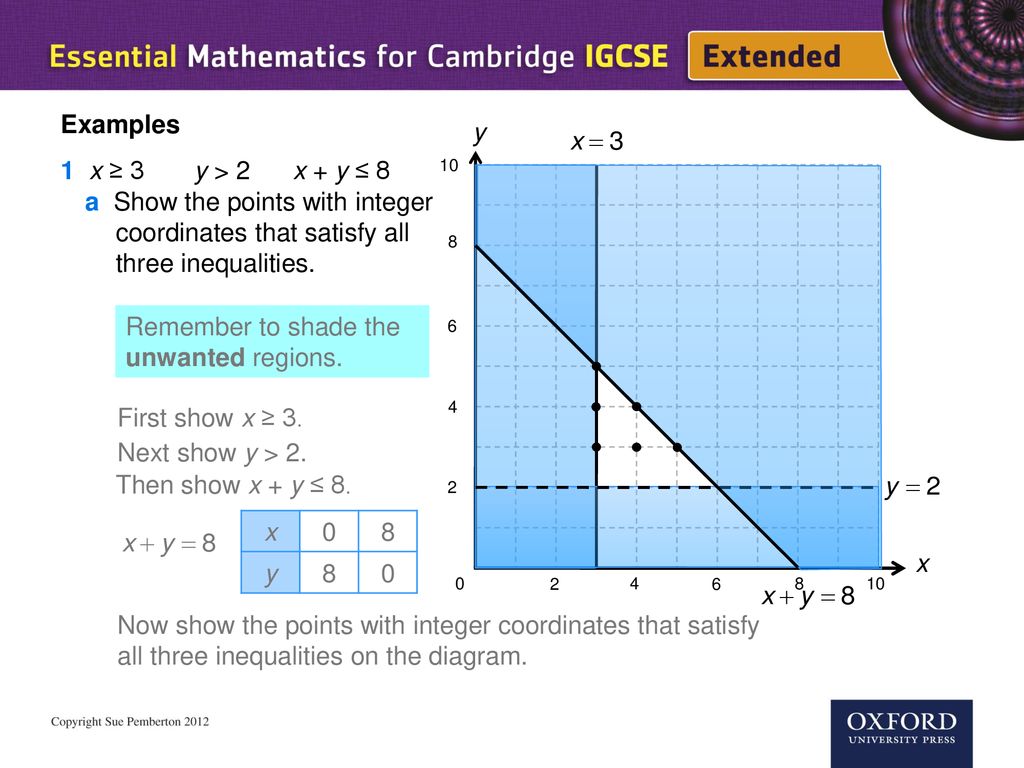
Linear Programming Ppt Download

In Which Quadrants Of The Coordinate Plane Is The Shaded Region Of The Inequality Located Y X Quora

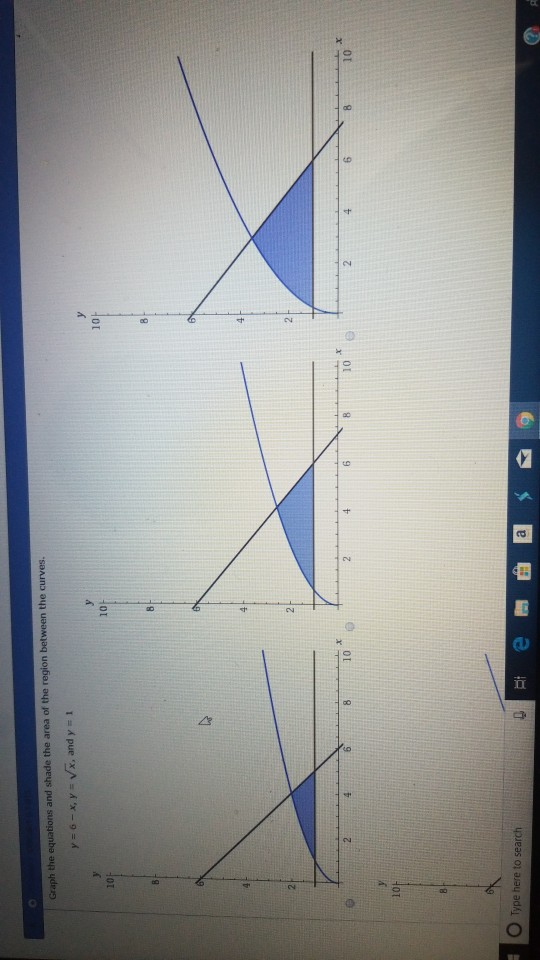
Graph The Equations And Shade The Area Of The Region Chegg Com

1 Consider The Following Equations Y X 2 4 Y X 5 X 0 X 2 Sketch And Shade The Region Bounded By The Graphs Of The Functions

Choose The Graph That Represents The Following System Of Inequalities Y 3x 1 Y X 3 In Each Brainly Com

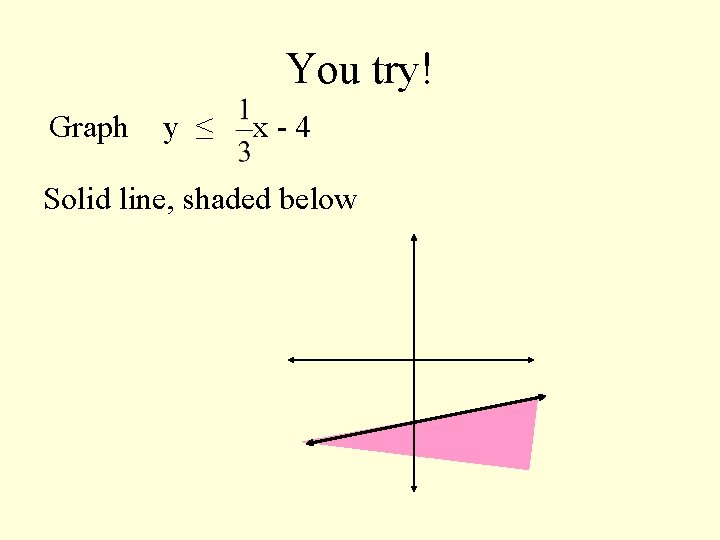
Algebra 6 5 Graphing Linear Inequalities Linear Inequality

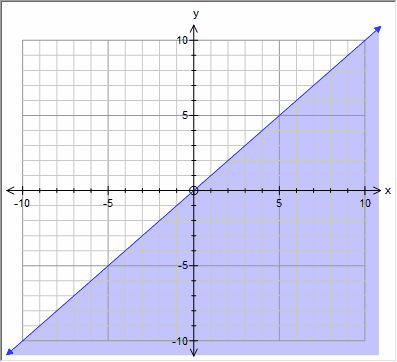
Graph Other Preferences

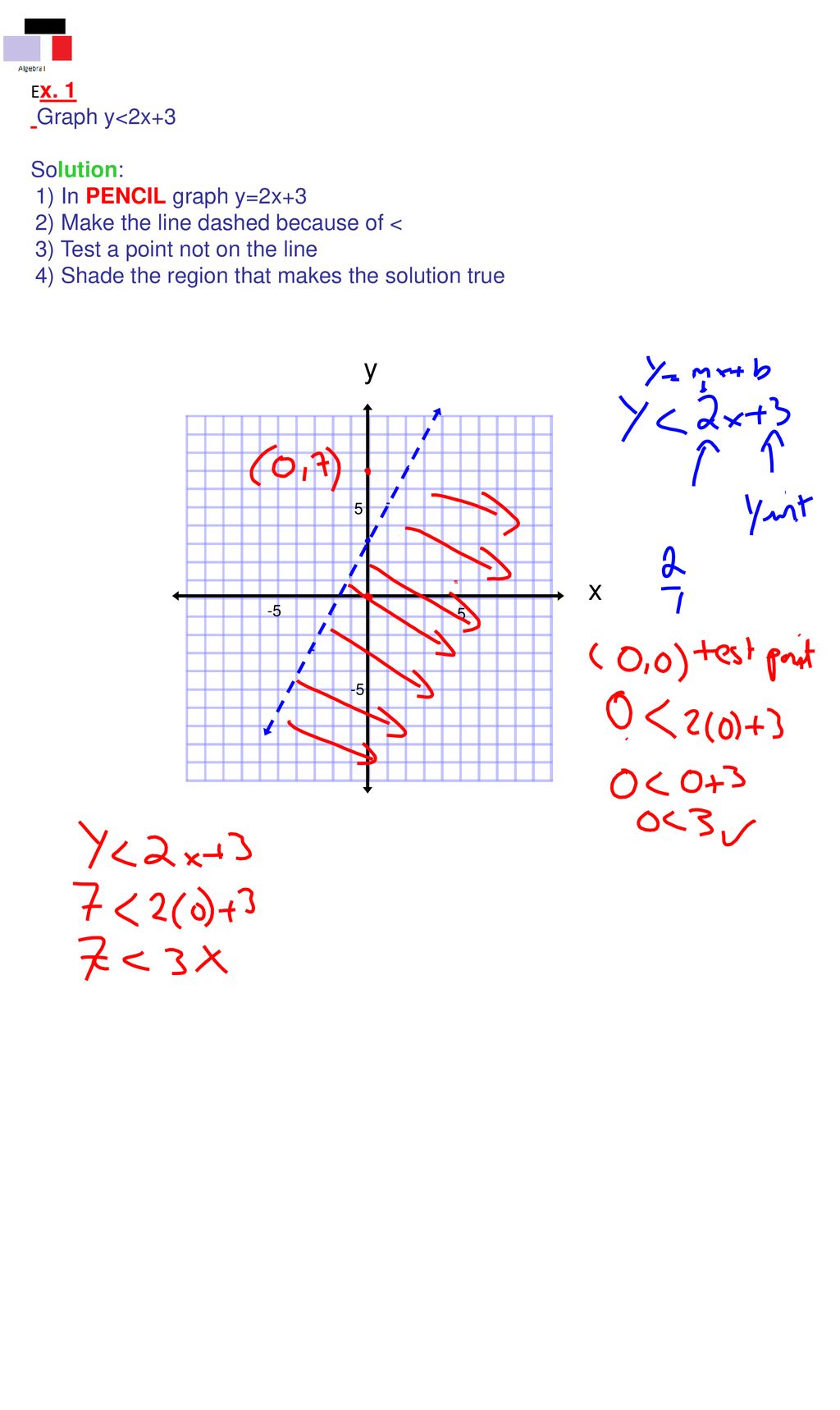
5 5 Linear Inequalities A Linear Inequality Describes The Region Of The Coordinate Plane That Has A Boundary Line Every Point In The Region Is A Solution Ppt Download

1

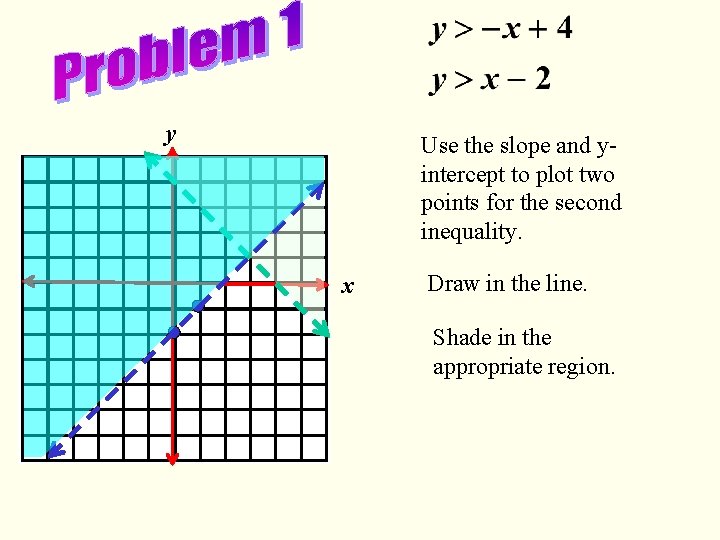
Look At The Two Graphs Determine The Following

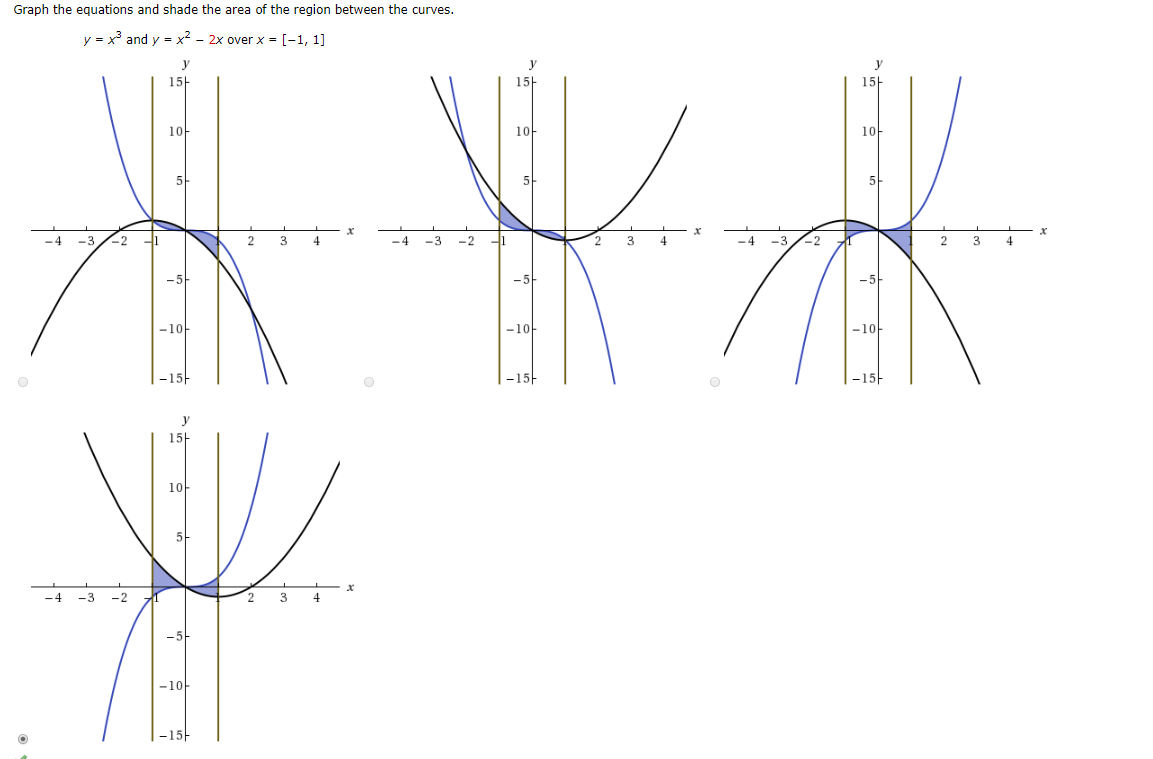
Graph The Equations And Shade The Area Of The Region Chegg Com

Graphing Inequalities Solutions Examples Videos

Incoming Term: y x graph shade,